|
Should it be possible to create a sort of
artificial gravitity/force? (for flying cars, skateboards, helicopters without
roters, propelling spacecrafts ..)
Let´s consider a rod turning
with a constant angular velocity, and a mass connected to this rod, that can
be moved alongside the rod.
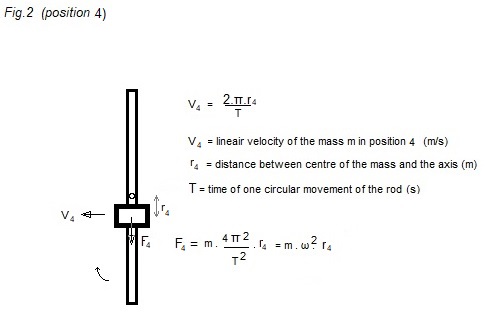
In position 1 the mass is at its greatest
distance r1 from the axis of the rod.

For example: m = 0,5 kg; r1
= 0,20 m; T = 0,1 s (10 revolutions/sec)
-> F1 = 394,8 N
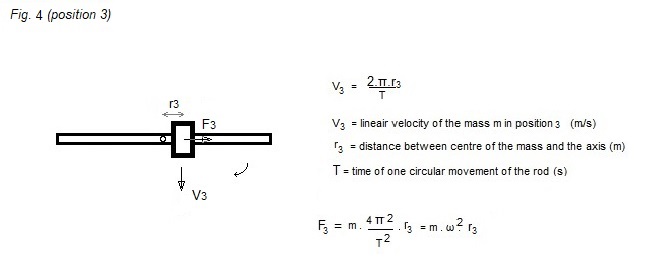
Now the rod has turned through
θ = 180 °
and the mass has been moved towards the centre.
For example: m = 0,5 kg; r2
= 0,05 m; T = 0,1 s (10 revolutions/sec)
-> F2 = 98,7 N
F1 - F2 =
296,1 N (= about 30 kgf)
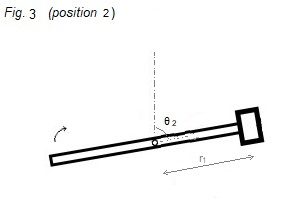
The rod has turned through an angle
θ2
from position 1 to position 2 with the
mass m still at its greatest distance r1 from the axis.
A mechanism connected at the rod (for
example a kind of electromagnet) starts pulling the mass m towards the
centre.
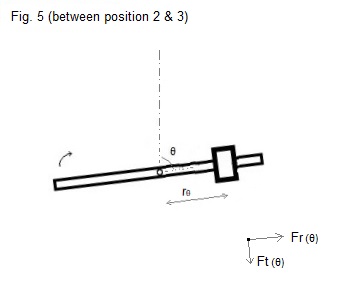
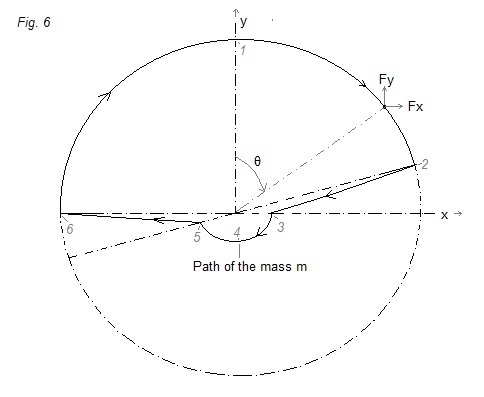
In figure 6 a possible path of mass m is
indicated (perhaps some points will be in reality a little bit more
smoothed, but I intuit that this is not so important).
If we express the path of the mass m as a function of time,
we should be able to calculate the force (as a function of time) that has to
be exerted on the mass m to oblige it to follow this path.
This force will be equal, but opposite in sign to the force
that the mass m exerts on the rod (on the axis of the rod)
.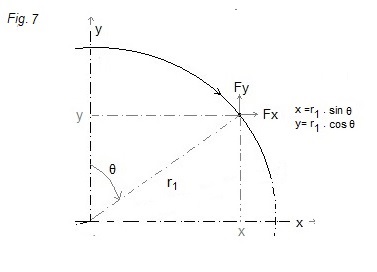
θ(t) = 360/(2π)
.
ω.t
(in degrees; ω = 2π/T ; T = time of one revolution; the angular velocity is
constant)
Programming in
Pascal/Delphi:
var m, r1,r2, T: real;
te2, te3, te5, te6 : integer; {angles teta}
mm: Tm_array;
Procedure Calculate;
var radius, radius0, sumax, sumay, tt,tt0, w,
dxdt, dydt, dxdt2, dydt2, x,y, Fx, Fy,
dxdt0, dydt0, dxdt20, dydt20, x0,y0, Fx0, Fy0,
teh, teh0, dtradius, dt2radius: real;
integraalFydt, integraalFxdt : real;
Fymean, Fxmean: real;
dd, dt: real;
te, q, cc: integer; {angle teta=te and angle fhi=q}
strh: string;
begin
T:=0.1; {10 rotations per sec}
w:=2*pi/T; {= 628,3 rad/s angular velocity in rad/sec}
m:=0.1; {0,1 kg}
r1:=0.2; {20 cm}
r2:=0.05; {5 cm}
te2:=50; {50 degrees}
te3:=90;
te5:=230;
te6:=270;
cc:=10; {to get a more accurate calculation}
sumax:=0; {for every degree the acceleration ax of m in the
x-direction is calculated; the program sums all the ax}
sumay:=0; {idem for the y-direction}
For te:=1 to (te2*cc) do {we choose that for te=80° = 0,44.pi the
mass m starts moving towards the axis: point 2 in fig.6; 1
degree=360/T =360 w/2pi sec)}
Begin
teh:=te/cc; {angle teta} {if te=100 then teh=1 degree, if te=8000
then teh=80 degree, with cc=100}
tt:= 2*pi* teh/(360*w); {time} {if teh=360 then tt=T, angular
velocity = constant, so tt = constant * teh}
x:= r1*sin(w*tt); {for example, te=7000 -> angle =70, tt= }
y:= r1*cos(w*tt);
mm[te].x:=x;
mm[te].y:=y;
dxdt:= w*r1*cos(w*tt); {speed}
dydt:= -w*r1*sin(w*tt);
mm[te].vx:=dxdt;
mm[te].vy:=dydt;
dxdt2:= -w*w*r1*sin(w*tt); {accelaration}
dydt2:= -w*w*r1*cos(w*tt);
sumax:=sumax+dxdt2; {dt=T/(360*cc} {after each dt the ax and ay is
calculated and all ax and ay are summed together}
sumay:=sumay+dydt2;
End;
For te:=(te2*cc+1) to (te3*cc) do {te2=50, te3=90}
Begin
dd:=te3-te2; {40}
teh:=te/cc; {if te=8001 then teh:=80,01 degree, with cc=100}
tt:= 2*pi* teh/(360 *w);
radius:=(r2+ (r1-r2)*( (te3- teh)/ dd ) ); {between 50° and 90º the
radius decreases proportionally with the angle (and so with the
time) }
dt:= T/(360*cc);
x:= sin(w*tt)*radius;
y:= cos(w*tt)*radius;
mm[te].x:=x;
mm[te].y:=y;
dxdt:=(mm[te].x-mm[te-1].x)/dt;
dtradius:= (-r1/dd+r2/dd)*360/T; {(-0.1*r1+0.1*r2)*360/T;} {de 1e
derivative}
dt2radius:= 0; {the 2e derivative}
{dxdt:= w*cos(w*tt)*radius + sin(w*tt)*dtradius;
dydt:= -w*sin(w*tt)*radius + cos(w*tt)*dtradius;}
dxdt2:= -w*w*sin(w*tt)*radius + w*cos(w*tt)*dtradius +
w*cos(w*tt)*dtradius+0;
dydt2:= - w*w*cos(w*tt)*radius - w*sin(w*tt)*dtradius -
w*sin(w*tt)*dtradius+0;
{sumax:=sumax+dxdt2;
sumay:=sumay+dydt2;}
End;
For te:=(te3*cc+1) to (te5*cc) do {te5=230}
Begin
teh:=te/cc;
tt:= 2*pi* teh/(360 *w) ; {if teh =180 then tt:= 0,05 is T/2}
x:=r2*sin(w*tt);
y:=r2*cos(w*tt);
dxdt:= w*r2*cos(w*tt);
dydt:= -w*r2*sin(w*tt);
dxdt2:= -w*w*r2*sin(w*tt);
dydt2:= -w*w*r2*cos(w*tt);
sumax:=sumax+dxdt2;
sumay:=sumay+dydt2;
End;
For te:=(te5*cc+1) to (te6*cc) do {te6=270}
Begin
dd:=te6-te5; {40}
teh:=te/cc;
teh0:=(te-1)/cc;
tt:= 2*pi* teh/(360 *w);
tt0:=2*pi* teh0/(360 *w);
radius:= (r1 - (r1-r2) * ((te6 - teh)/dd) ); {between 230° and 270º
the radius increases proportionally with the angle and so with the
time}
radius0:= (r1 - (r1-r2) * ((te6 - teh0)/dd) );
dtradius:= (r1/dd - r2/dd) *360/T; { (0.1*r1-0.1*r2)*360/T;}
x:= sin(w*tt) * radius;
y:= cos(w*tt) * radius;
x0:= sin(w*tt0) * radius0 ;
y0:= cos(w*tt0) * radius0;
dxdt:= (x-x0)/(tt-tt0); {w*cos(w*tt)*radius+sin(w*tt)*dtradius}
dydt:= (y-y0)/ (tt-tt0); {-w*sin (w*tt)*radius+cos(w*tt)*dtradius;}
dxdt2:= -w*w*sin(w*tt)*radius + w*cos(w*tt)*dtradius +
w*cos(w*tt)*dtradius + 0;
dydt2:= -w*w*cos(w*tt)*radius - w*sin(w*tt)*dtradius + -
w*sin(w*tt)*dtradius + 0;
{ sumax:=sumax+dxdt2;
sumay:=sumay+dydt2; }
End;
For te:=(te6*cc+1) to (360*cc-1) do
Begin
teh:=te/cc;
tt:= 2*pi* teh/(360 *w) ;
x:=r1*sin(w*tt);
y:=r1*cos(w*tt);
dxdt:= w*r1*cos(w*tt);
dydt:= -w*r1*sin(w*tt);
dxdt2:= -w*w*r1*sin(w*tt);
dydt2:= -w*w*r1*cos (w*tt);
sumax:=sumax+dxdt2;
sumay:=sumay+dydt2;
End;
{suamay = cc*360 }
Fy:=m*sumay; {= m * (dFy1+dFy2+dFy3+....) }
Fx:=m*sumax;
integraalFydt:=Fy*(T/(360*cc)); {= dFy1*dt+dFy2*dt+... =
(dFy1+dFy2+..)*dt = Fmean * T} {dt=T/(360*cc}
integraalFxdt:=Fx*(T/(360*cc));
Fymean:=integraalFydt/T;
Fxmean:=integraalFxdt/T;
str(Fymean:0,strh);
form1.label2.caption:=strh;
str(Fxmean:0,strh);
form1.label3.caption:=strh;
end;
procedure TForm1.Button1Click(Sender: TObject);
begin
Calculate;
end;
end. |
We´ll get a net accelarion upwards?
Let´s run the
program and find out ... ??????
The result are strange values.. probably cause:
when the mass starts to move towards the centre, the speed alongside the
radius has suddenly a value, which in reality is not possible. It should
feel an accelaration towards the centre and increase the speed towards the
centre as a function of time, and later on get a deaccelaration and then
slowly approaching the centre.
----------------
Let´s calculate the following: (should be quite easy
to contruct..)

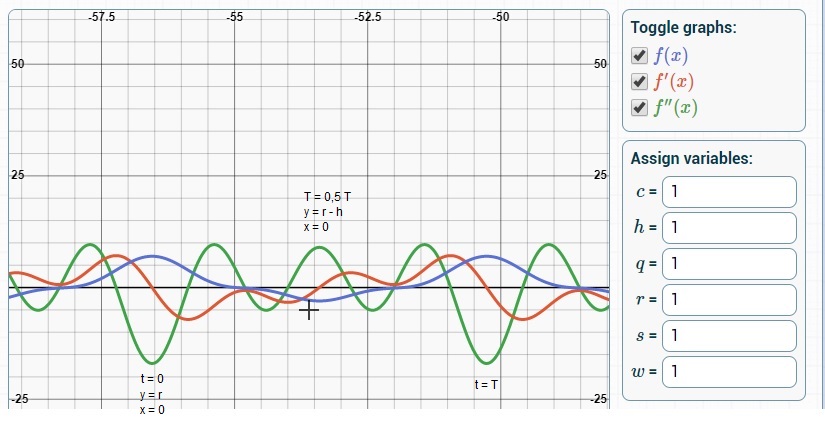
The mean accelaration in the y-direction is the integral of f"(t) dt over T
= > the surface of ff" under the horizontal axis = the surface of ff" above
the horizontal axis.
f´(t) is the
primitive function of f"t), if you follow the red curve of f´(t) you will
see easily that the surface under = surface above over one period T.
=> the mean
accelaration in the y-direction = zero
Newton's first
law holds ...

https://www.derivative-calculator.net/
https://patents.google.com/patent/US3683707A/en (a device to
convert a circular movement into a linear force)
https://www.youtube.com/watch?v=r7NPx3dRpUw
https://www.youtube.com/watch?v=obnxoJsBDGQ
14 February
2020
by
Rinze
Joustra www.valgetal.com

|








