Unlimited energy by means of flexibele werkvormen (accordion-shaped volumes) ?
http://nl.wikipedia.org/wiki/Wessel_di_Wesselli
https://www.vice.com/read/raw-power-860-v16n4
Letīs try to demonstrate that itīs not possible that a constant water pressure can increase the volume of an object submerged under water.
We will do calculations to the object whose cross section is shown below.
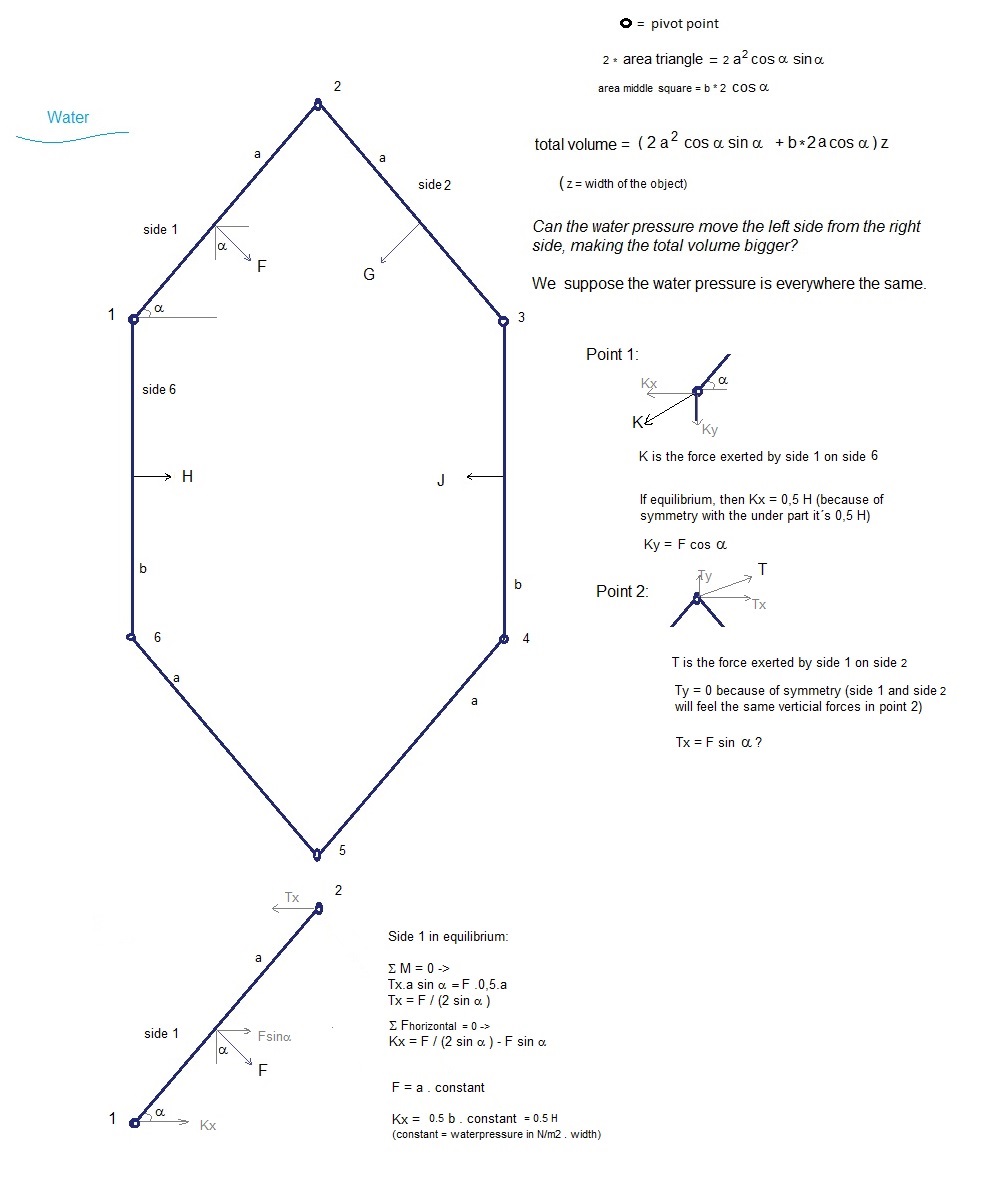
We want to move point 1 to the left, so that the middle cubic volume becomes bigger:
a < 45 š
This happens when 0,5 b < a/(2 sin a) - a sin a
What happens then with the total volume?
Total volume = 2 a2 cos a sin a + b.2a.cos a (letīs assume the width is 1 mtr)
First -> b = a/( sin a) - 2.a sin a -> Total volume = 2 a2 cos a sin a + 2a2 cos a/ sin a - 4 a2 cos a sin a = 2 a2 cos a sin a (-1 + 1/ sin2a)
Letīs take a = 40 š -> b = a ( 1/( sin a) - 2sin a )-0.01a = a . (0,270-0.01) = 0,26 a
So with a = 40 š and b = 0,26 a the forces excerted by the water pressure on the oblique sides (1, 2, 4 and 5) are in equilibrium with the forces excerted by the water pressure on the vertical sides 3 and 6.
Letīs now make b a little bit smaller, for example, b = 0,23a. There will be no equilibrium and the water pressure on the oblique sides will then move the vertical side 6 to the left and the vertical side 3 to the right. Will the total volume then become bigger??
a = 40 š and b = 0,23 a -> total volume = 2 a2 cos a sin a + b.2a.cos a = a2 (2cos40sin40 + 0,46 cos40) = 1,337 a2
a = 39 š and b = 0,23 a -> total volume = a2 (2cos39sin39 + 0,46 cos39) = 1,336 a2
a = 38 š and b = 0,23 a -> total volume =a2 (2cos38sin38 + 0,46 cos38) = 1,333 a2
It is a pitty, but the volume becomes smaller...
So it seems to be that we can
not construct a perpetum mobile..
![]()
Mr. Wessel di Wesselli did
visit the HTS Leeuwarden /TU Twente in 1985. I was there and I did like very
much his "performance".
It was curious that more or less the only argument against him
was "this is not according the law of conservation of energy".
But this law cannot be
proved... Only until now not any experiment did demonstrate the contrary.
Mr. Wessel di Wesselli still
seems to be active, which is fine. ![]()
15 June 2015 by Rinze Joustra
www.valgetal.com