length: 1 mtr
diameter: 50 cm
B = 1 tesla

B = μ₀ . N/l . I   (see  hyperphysics)

N= amount of windings
l=length
μ₀ = 2.10^-7 N·A⁻²

I = B . l /(μ₀ . N)

B = 1 T, l = 1 m, N = 1000 -> I = 1 . 1 / (2.10^-7  .1000) = 5000 A , very high..

In www.gmw.com/electromagnets , amonst others, an electromagnet (coil) is sold: B= 0,13 T , DC power = 5,18 kW (140 A, 37 V), water cooling 12 ltr/min, 360 turns.  Not exactly what we need, but just to get an idea. Not enough magnetic field, consuming a lot of power and also very expensive . Another example: http://www.gmw.com/electromagnets/dipole/5503/5503.html (30 cm gap, 140 A, 11,5 kW, 0,3 T,  16 ltr/min water cooling, about 60000 $)
 

Electromagnets are usually in the form of iron core solenoids, see hyperphysics .
The internal magnetic domains line up and multiplicate the field by factors to even thousands.

I think it would be better to place an electromagnet with an inner core, on top of the fusor and under the fusor (or if we turn it 90 º, at the sides).

In the next link a permanent magnet, with dimensions 11x9x2 cm and a magnetic field (Remanencia Br) of 1.3 T is sold for about 120 €, see:  https://www.supermagnete.es/imanes-bloque-neodimio/bloque-magnetico-110.6mm-x-89mm-x-19.5mm-neodimio-n45-con-recubrim-epoxi_Q-111-89-20-E

Using a couple of permanents magnets?
They seem to loose rapidly strength with the distance, see: Fieldcalculator.asp
A small disk of 10 cm diameter and 1 cm thickness has at 1mm distance B= 1,4 tesla, but at  10 cm distance B=1,9 gauss, and at 30 cm B=0,1 gauss.

A small disk with the characteristics as in fig.1:

Fig.1a. The magnetic field of a small cylindrical neodymium magnet

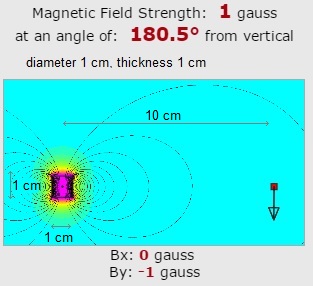
If our SEM fusor had a diameter of 20 cm and a length of 0,5 m, the circumference would be 62 cm.
We could place 60 of this small magnets in a ring around. The magnet field in the middle would be 60 gauss; not enough.
The price of one such small disk is about 20 $.  ( kjmagnetics.com ). One ring would cost 1200 $. 50 rings... far to expensive.. Not an option.

A small cube of 1 x 1 x 1 cm

Fig.1b. The magnetic field of a small cubical neodymium magnet

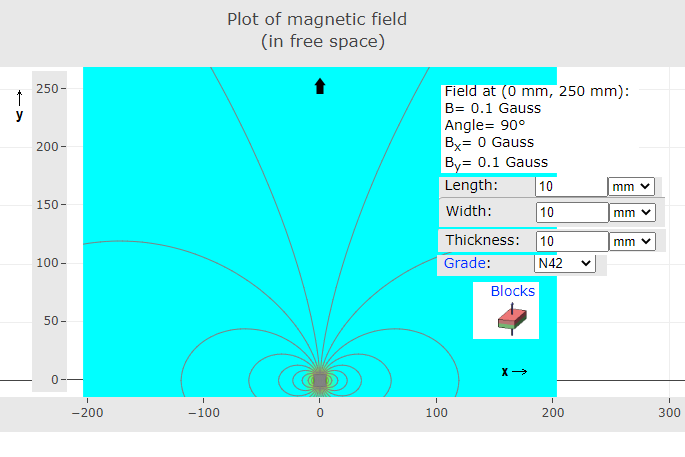
Assume we want to have a magnetic field of 0,5 T  in the centre of the  vacuum chamber of the Sem Fusor which has a length of 50 cm.
0,25 T is produced by an amount of small magnets under, and 0,25 T is produced by an amount of small magnets above the vacuum chamber.

0,25 T / (0,1 .10^-4 T  ) = 25000 small magnets.

In www.supermagnete.es/imanes-bloque-neodimio  A cube of 10 x 10 x 5 mm costs 0,83 € (N42)

We would need of these  about 25000 x 2  x 2  = 100 000 magnets  x 0,83 € = 83 000 €

11.4 fig 1b screenshot.png

A bit expensive..

I think the best idea is to contruct a vacuum chamber with our experiment and  to look for an existing magnet in, for example, an university or company. (universidad de Zaragoza?)

Or perhaps here? 

https://ofertas.clinicpoint.com/zaragoza/offer/7577/resonancia-magnetica-de-alto-campo

(Consider the SEM fusor with a diameter of 45 cm and a length of 100 cm.
We make small electromagnets winding copper wire around a iron bold.
These electromagnets are placed around the vacuum chamber of the SEM fusor.)
 

Fig.2. The magnetic field of a electromagnet with an iron core

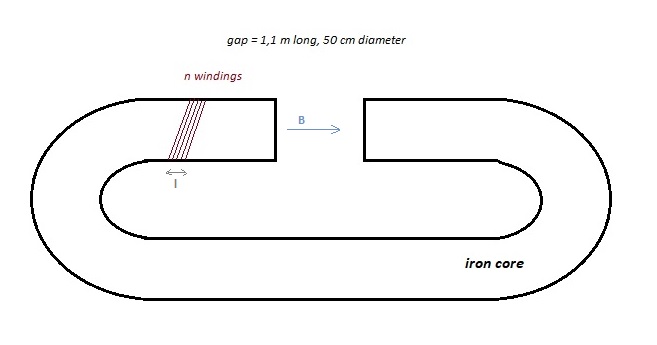
Volume of the iron core = π (0,25)² .  10  (for the length of the iron core  we take 10 m)

= 2 m³  specific mass of iron is about 7 mt/m³ ->  mass of the iron core = 14 mt

Price of iron about 1 till 3 € / kilo?

For a coil:  B =  μ₀ . N/l .I
N = amount of windings
l = length of the windings
I = current through the windings

µ₀= permeability of free space = 4π × 10⁻⁷ N·A⁻² 

The iron core causes an increase of the magnetic field inside the coil of about a 1000 times.

According wikipedia.org/wiki/Electromagnet   (see also: web.mit.edu/6.013_book/www/chapter9/9.7.html )
(and page 706 Physics Alonso & Finn)

N. I = B ( L_core/μ + L_gap/μ₀ )  (assuming that B in the core and in the gap are the same, that no B (flux) is escaping, that the gap is relatively small, L= length)

B = 1 tesla,  L_gap = 1,1 m     N.I = 1. ( L_{core /}  (6.3 10⁻³ ) + 1,1 / (4π × 10⁻⁷ ) ) =    8,8.10⁵  Ampere turns.   (neglected the L_{core /}  (6.3 10⁻³ ) term)

Engineeringtoolbox.com/permeability - > iron 99,8% pure -> μ_iron = 6.3 10⁻³ mkg^-2C  ,   μ_{iron /} μ₀ = 5000

The length of the iron core is not so important.

Electrical cable in Bricodepot.es:  2,5 mm² -> 0,22 € / m

According Engineeringtoolbox.com  the maximum current of such a cable is about 20 A. ->  8,8.10⁵  = N. 20 -> N = 44000 turns.
diameter of a turn = 60 cm -> circumference = 2π.0,3 = 1,89 m -> total length = 44000 . 1,89  m = 83 10³ m - > price = 18000 € ..

Fig. 3.

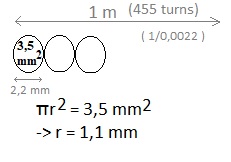
If we take into account the insulation material around the cable (thickness of it is aproximated) and suppose the area of the cross section is then 3,5 mm2, then we can make over 1 meter length 1 layer with 455 turns.

To get 44000 turns, we need about 100 layers. The thickness of all layers would be around: 22 cm.

For copper the resistivity ρ = R . A/l  = 1,68 . 10^-8  ohm meter  (R = electrical resistance, l = length, A = cross-sectional area)

Diameter vacuum chamber = 50 cm, diameter coils = about 60 cm

R =  ρ . l / A  = 1,68 . 10^-8 . 44000 . 2. π . 0,30 / (  2,5 . 10^-6  )     = 557 ohm

Electrical power generated = I² . R = 20² . 557 = 224 kW (about 200 electrical heaters of 1000 W)

Quite difficult to realize..

Back to main page

    Rinze Joustra        www.valgetal.com