Binomial distribution

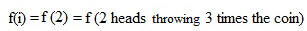
Understanding binomial distribution

Wikipedia.org/wiki/Binomial_distribution

Investopedia.com/terms/b/binomialdistribution.asp

The binomial distribution is a probability distribution that summarizes the likelihood that a value will take one of two independent values under a given set of parameters or assumptions. The underlying assumptions of the binomial distribution are that there is only one outcome for each trial, that each trial has the same probability of success, and that each trial is independent of each other.

Example:

Throwing three times a coin, n=3 (the n=3 times of doing the experiment are independent)

A = head

p = P(A) = 0,5

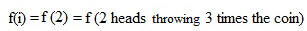
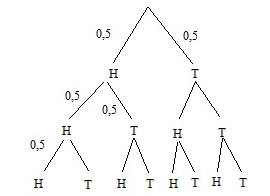
The sample space = { HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}

In the tree diagram you can see that there are 3 possibilities of getting 2 heads {HHT, HTH, THH} out of totally 8 possibilies.

There are 3 places to put a H or a T. We choose 2 places out of 3 =>

So f(2) = 3/8 = 0,375

The general formula is:

Just imagine a tree diagram with n times a choise "k" with change p and "not k" with change (1-p).

This is the way I understand the binomial distribution. I hope this explanation is useful for somebody. Anyway it is for myself, to refresh my memory sometimes in the future ☺

In Mathsisfun.com/data/binomial-distribution.html there is a more extensive explanation.

Rinze Joustra