
Simple way of understanding a combination
In mathematics, a combination is a way of selecting items from a collection, such that (unlike permutations) the order of selection does not matter. (see Wikipedia)
For example:
We have a collection with the numbers 1 till 5 and we choose a subset of 3 numbers out of this collection. The order does not matter.
First we can choose out of 5 numbers:

After having chosen "1" we can choose "2", "3", "4" or "5":
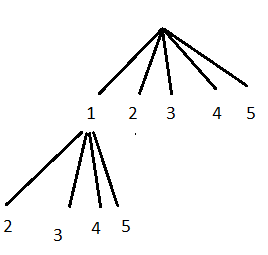
After having chosen "1" and "2" we can choose "3", "4" or "5":
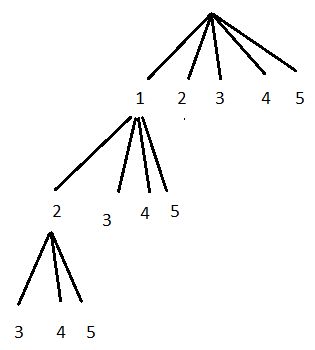
So we can have [1,2,3], [1,2,4] or [1,2,5]
The total number of subsets is:
5 x 4 x 3 = 60 (this the way multiplying is explained in elementary school: 4 groups of 3 = 12 and 5 groups of 12 = 60 = 5x4x3)
But many of these subsets are the same, because the order does not matter: [1,2,3],[1,3,2], [2,1,3], [2,3,1] [3,2,1], [3,1,2] ... These are called permutations.
The number of permutations of 3 elements is: 3 x 2 x 1= 6 (you could make a same tree diagram as above).
The total number of subsets: 60 = C x 6
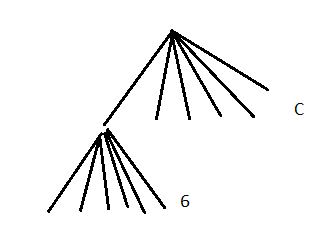
We have:
6 of [1,2,3],[1,3,2], [2,1,3], [2,3,1] [3,2,1], [3,1,2]
6 of [4,2,3],[4,3,2], [2,4,3], [2,3,4] [3,2,4], [3,4,2]
6 of [5,2,3],[5,3,2], [2,5,3], [2,3,5] [3,2,5], [3,5,2]
etc.
Totally we have C groups of 6 = C x 6
In the first branch we have all permutations of [1,2,3], in the second branch we have all permutations of [2,3,4] etc.
The amount of combinations is now C = 60 : 6 = 10 = 5x4x3 / 3x2x1 (dividing is the contrary of multiplying, as explained in elementary school..)
amount of combinations = 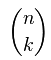 =
=
![]() = 5 x 4 x 3 / (3x2x1) (in our example)
= 5 x 4 x 3 / (3x2x1) (in our example)
This is the way I understand the formula of combinations. I hope this explanation is useful for somebody. Anyway it is for myself, to refresh my memory sometimes in the future ☺
Rinze Joustra