Proof that the golden ratio is irrational by contradiction
What is the golden ratio is good explained in Wikipedia.org/wiki/Golden_ratio
Summary:
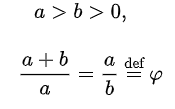
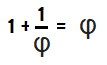
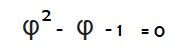
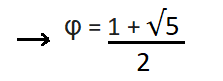
Proof by contradiction:
Letīs assume that φ is rational.
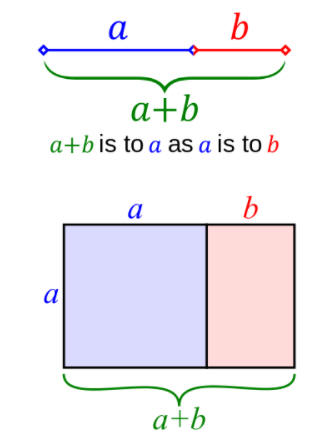
a/b = φ is completely reduced, so its greatest common divisor is 1 ( gcd(a,b) = 1 )
For example, 4/8 can be reduced to 1/2
b < a (from definition)
a/b = (1+ √5)/2 < ( 1 + √9) / 2 = 2 → a < 2 b
a/b = = (1+ √5)/2) > (1+ √4)/2 = 3/2 → a > 3/2 b (not necessary..)
a < 2 b → a - b < b
From 1/φ = φ - 1
→ b/a = a/b -1 = (a - b)/b
→
,
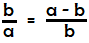with a-b < b and with b < a
b/a is completely reduced, but is equal to another fraction with both a smaller denominator and a smaller numerator. (For example, 3/4 = 2/3)
This is a contradiction, so φ is not rational.
I hope this is useful for somebody. Anyway it is for myself, to refresh my memory sometimes in the future ☺
Rinze Joustra